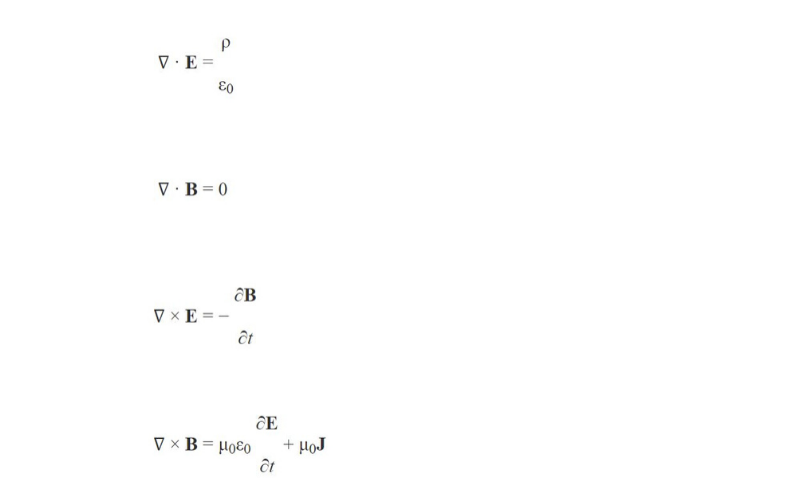Breathtaking Maxwell Fourth Equation In Differential Form

Maxwells Equations and their derivations.

Maxwell fourth equation in differential form. The Fourth Maxwells equation Amperes law The magnitude of the magnetic field at any point is directly proportional to the strength of the current and inversely proportional to the distance of the point from the straight conductors is called Amperes law. First equation is nothing but the Gausss law. Hello friends today we will discuss the Maxwells fourth equation and its differential integral form.

The equation 13 is the Differential form of Maxwells fourth equation or Modified Amperes circuital law. In this video i have explained Maxwells 4th equation with Integral and Differential form or point form with following Outlines0. We will convert Maxwells four equations from integral form to differential form by using both the Divergence Theorem and Stokes Theorem.

D displacement current The equation 13 is the Differential form of Maxwells fourth equation or Modified Amperes circuital law. The differential form of Maxwells equation is beyond higher secondary level because we need to learn additional mathematical operations like curl of vector fields and divergence of vector fields. These equations can be written in differential form or integral form.

So we focus here only in integral form of Maxwells equations. The Divergence Theorem In other words it equates the flux of a vector field through a closed surface to a volume of the divergence of that same vector field. The general laws of nature are to be expressed by equations which holds good for all systems of coordinates that is are covariant with respect to any substitution whatever generally covariant BP94.

Maxwell 4th Equation of Electromagnetics in differential form using Displacement current and Modified Amperes Circuital Law is discussed. Differential form maxwell fourth equation. Let us first derive and discuss Maxwell fourth equation.

Posted on January 31 2012 September 14 2018. This law was developed by André-Marie Ampère in 1826 and related the magnetic field B associated with an electric current passing through a wire as illustrated in the diagram. I chose the topic ignorant of how the differential form of these equations are used and I cannot seem to find a digestable use of their differential form anywhere.